[Data Science] Machine Learning - Decision Tree

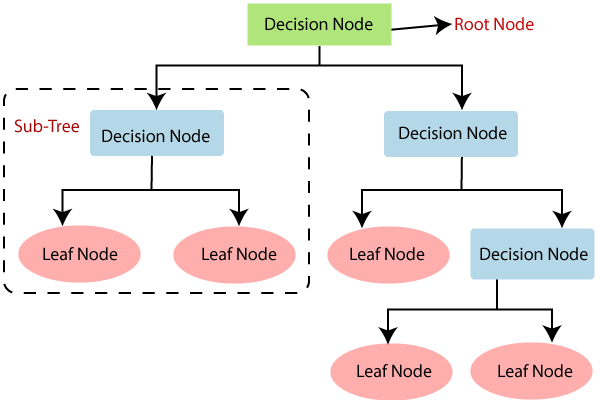
Decision Tree

Decision Tree 는 Root Node를 시작으로 Decision Node를 기준으로 데이터를 분류하는 기법입니다. Decision Node에서 분류가 완료되면 Leaf Node에 도달하게되고 분류가 완료가 됩니다.

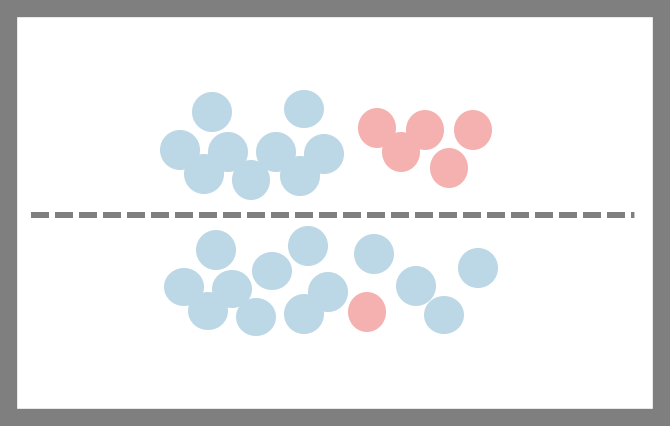
불순도 & 엔트로피

불순도는 분류된 데이터가 얼마만큼 섞여 있는지를 의미합니다. 하기그림을 보면 점선을 기준으로 위쪽은 두개의 데이터가 많이 섞여있고 아래에는 조금 섞여 있습니다. 불순도를 따지자면 위쪽이 불순도가 높고 아래가 불순도가 낮다고 표현합니다.

엔트로피 란 불순도를 수치적으로 표현한 척도입니다.

\[Entropy = -\sum_{i=1}^{m} (p_{i})log_{2}(p_{i})\]

불순도가 높으면 엔트로피는 1에 수렴하고 낮으면 0에 가까워 집니다.

상기 그림에서 엔트로피를 구해보도록 하겠습니다. 하늘색이 22개 빨간색이 6개이며 엔트로피를 구하면 하기 수식이 나옵니다.

\[-[\frac{22}{22+6}(log_{2}(\frac{22}{22+6})] -[\frac{6}{22+6}(log_{2}(\frac{6}{22+6})]\]

그렇다면 회색 점선처럼 분류된 후의 엔트로피를 구해보도록 하겠습니다. 두 개 이상의 영역의 대한 엔트로피는 하기와 같습니다.

\[Entropy(A) = \sum_{i=1}^{d}R_{i}(-\sum_{k=1}^{m} (p_{i})log_{2}(p_{i}))\]

여기서 Ri 는 분할전 데이터 가운데 분할후 i 영역에 속하는 데이터 비율입니다.

\[-\frac{14}{14+14}[(\frac{22}{22+6}(log_{2}(\frac{22}{22+6}))] - \frac{14}{14+14}[\frac{6}{22+6}(log_{2}(\frac{6}{22+6}))]\]

정보획득 (Information gain)

정보획득이란 분류이전의 엔트로피와 분류이후의 엔트로피 변화량을 의미하여 수식으로 나타내면 하기와 같습니다.

\[Information gain = entropy(parent) - [weighted average] entropy(children)\]

정보획득량이 많아질수록 불순도가 내려가 최적의 분류가 된다고 보면됩니다.

상기 개념을 코드로 구현해보도록 하겠습니다. 이전시간에 사용하였던 SVM 코드를 그대로 사용하여 모델을 하기와 같이 변경해주면 됩니다.

from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier()
model.fit(x_data_sample, t_data_sample)